
[ad_1]
The probabilistic method to self-locate below uncertainty
Desk of contents:
- What’s localization and why does a robotic want it?
- Why are probabilistic instruments used to compute localization?
- Finish-to-end instance: the right way to use bayesian algorithms to find out a robotic’s place below uncertainty?
How can autonomous automobiles keep inside a single lane at 60mph? How can an i-robot keep away from falling down the steps? How can supply robots know if they will the precise hungry buyer? These are just some of the questions autonomous autos should reply with out human intervention.
1. What’s localization? And why does a robotic want it?
As you may think, correct car location is important as to if the autonomous car successfully and safely completes its duties. The method to estimate the car’s place from sensor information is named localization. Localization accuracy will increase with sensors that add info and reduces with the car’s motion which provides noise.
2. Why are probabilistic instruments used to compute localization?
Probabilistic instruments may be leveraged to enhance location accuracy the place neither the sensors nor the motion is 100% correct.
What’s chance?
In keeping with the dictionary definition, chance is a “numerical description of how possible an occasion is to happen” (wikipedia). Nonetheless, with regards to the which means of chance, the reply just isn’t that straightforward. There are rivaling interpretations to chance from two main camps, the frequentists and bayesians.
The Frequentist method interprets chance because the relative frequency over time; what number of occasions will I get my desired consequence if I repeat an experiment many occasions?
This method is goal as a result of anybody who runs the experiments (e.g. flipping a coin) will get the identical end result within the lengthy run.
The Bayesian method interprets chance because the diploma of certainty that an occasion will occur. How sure am I that I’ll get my desired consequence given skilled data and the obtainable information? This method is subjective, because it represents the present state of perception by combining (subjective) earlier data and experimental information identified thus far. It permits estimating the chance of a singular occasion that we will’t run many occasions, the place the frequentist which means doesn’t apply.
For instance, if the chance {that a} date texts you again after your first meetup is 0.8, then we’re 80% sure that you just had a good time and the individual will textual content you again; we don’t imply they are going to textual content 80% of the time for those who repeat the primary date time and again once more.
What are the advantages of bayesian chance?
Bayesian chance permits us to each quantify our diploma of perception and to replace it in gentle of recent proof.
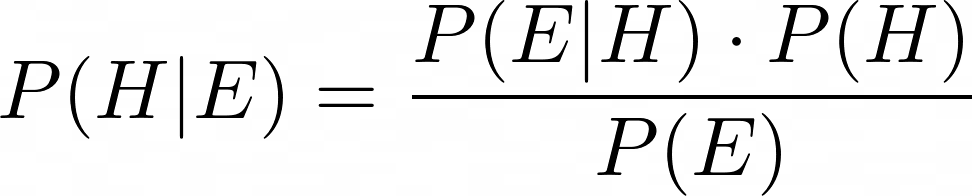
In our context, P(H) is our preliminary guess of the robotic‘s place, and P(H|E) is our up to date guess after measuring the sensors’ proof E.
The speculation chance distribution quantifies our certainty within the robotic’s place.
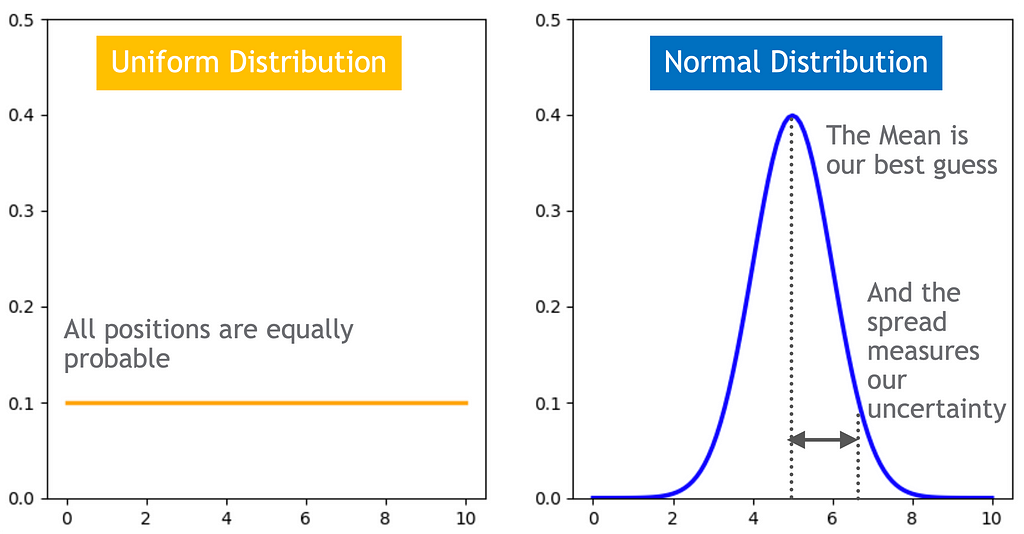
The speculation can change based on proof
The extra informative and correct the sensors information, the larger impact it is going to have. If the sensor is ideal, the robotic’s place will align with the sensor’s studying, in any other case if the sensor information could be very noisy or non-informative, the robotic’s place will keep the similar.
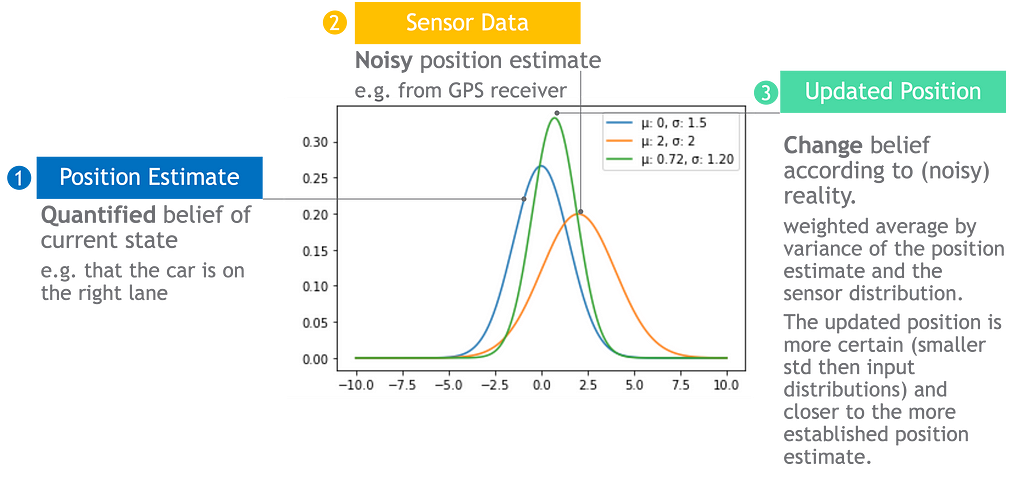
Updates can mix a number of sources of proof
We are able to formulate Bayes’ legislation to mix a number of information sources by utilizing the chain rule, often known as the overall product rule. It permits simplifying a joint distribution of a number of proof to a product of conditional possibilities.
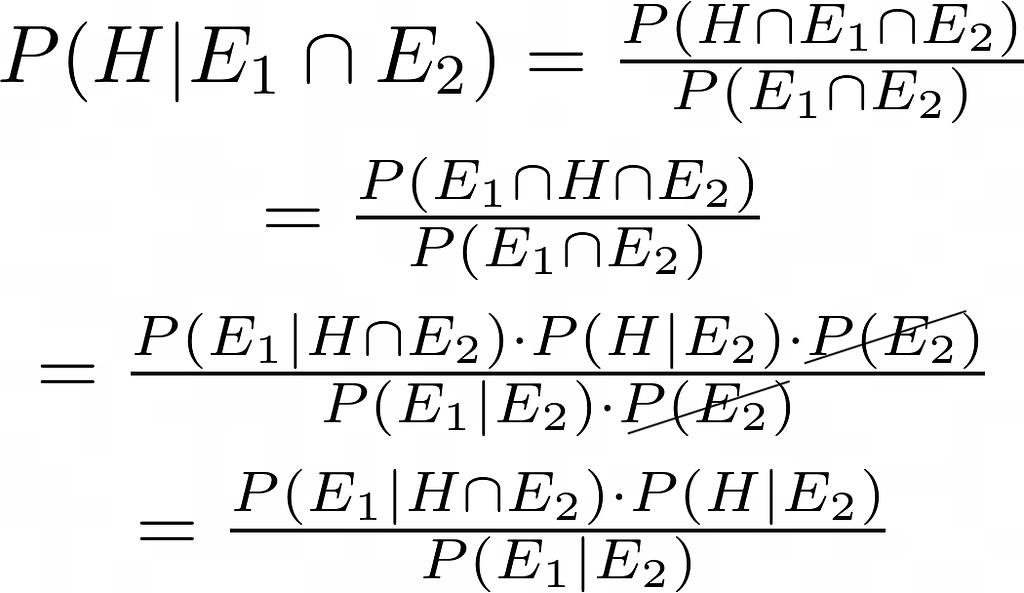
For instance, we regularly use GPS to navigate from our present location however GPS works greatest in clear skies and its accuracy is restricted to some meters. Autonomous automobiles can’t solely depend on GPS to stay in a lane that may be a few meters vast and to navigate in tunnels or underground parking tons. Autonomous autos can compensate for GPS deficiencies by including extra sources of data similar to cameras.
3. Finish-to-end instance: the right way to use bayesian algorithms to find out the robotic’s place below uncertainty?
Let’s take a deep dive right into a bayesian filter that recursively improves localization chance estimates utilizing bayesian inference. The recursive nature signifies that the output of the filter at time t_0, P(H|E), serves because the speculation enter for the subsequent timestamp t_1, P(H).
Suppose a supply robotic is looping a round path inside an area station to move provides. The robotic has a map detailing the lay of the land and the situation of sensors.
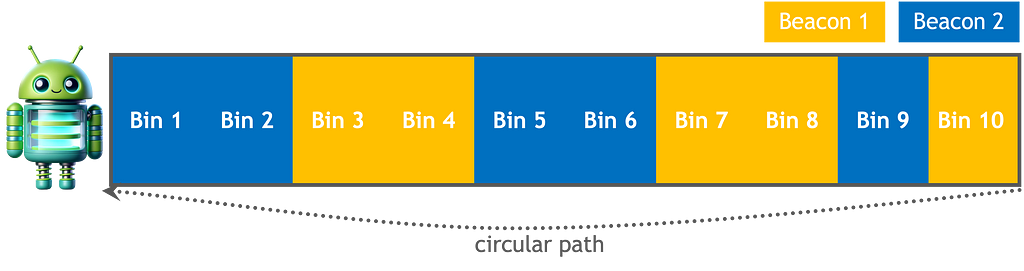
– Downside definition:
We check with the estimated robotic location because the robotic’s state house. For instance, a two-dimensional vector (i.e. an ordered pair of numbers) tracing x-axis place and x-axis velocity can observe a robotic location and altering pace in one-dimension. It’s potential to increase the robotic’s state house to extra dimensions to trace a number of place dimensions (y, z), orientation, and so on.
For simplicity, we will assume our robotic is shifting with fixed pace. The motion provides uncertainty to the computation, since it’s not 100% dependable. The engine would possibly fail to run at a selected velocity or the robotic would possibly encounter obstacles, which is able to trigger the robotic to overshoot or undershoot its anticipated motion.
Our robotic will sense its location by measuring the presence of a beacon. The sensor readings, additionally referred to as measurement house, aren’t 100% correct. Sensors would possibly confuse noise with a beacon sign that may result in false alarms or fail to detect a sign at all.
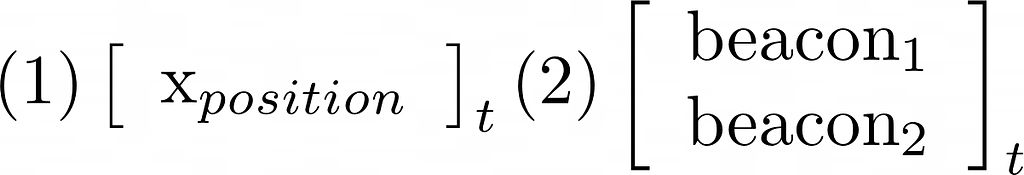
– The algorithm: histogram filter
With this bayesian filter the robotic state house is represented by a histogram by a finite variety of bins or areas. It’s a discrete filter, which means the robotic can solely be in one in every of these areas, and we compute the chance that the robotic is in every. Moreover, inside every bin, similar to a 5 sq. meter space, the chance of being at any particular level is identical. If we need to enhance the granularity, we should add extra bins.
This filter is non parametric, which means it doesn’t make any sturdy assumptions on the robotic’s state illustration, and isn’t restricted to 1 sort of distribution similar to a Gaussian. It is ready to symbolize complicated location estimates, similar to a multimodal speculation that retains a number of greatest guesses, but it surely comes with a computational value — an exponential complexity. So as to add a further dimension, from 1-D to 2-D whereas protecting the identical granularity, we are going to want 10×10 bins, to maneuver to 3-D we are going to want 10x10x10 bins, and so forth. This can be a vital limitation for robots that observe a number of dimensions and are restricted in reminiscence and compute energy.
– Calculation:
- Preliminary guess: We begin from an unknown location outfitted with a map. In the beginning each area is equally possible, as represented by a uniform distribution throughout all bins.

2. Motion perform: simulates the robotic motion. The robotic’s movement is stochastic, which means it’s not assured to maneuver to the specified bin at every time step. To replace the robotic’s location after every transfer, we calculate the chance of the robotic being in every area on the subsequent time step. This calculation considers each the chance of the robotic to remain in the identical area and the chance of it to maneuver to a unique area.
For every motion:
For every area:
Area chance at time t+1 =
Area chance at time t x keep chance +
Likelihood of robotic coming from the neighboring area x transfer chance
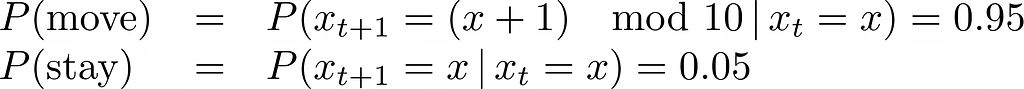
As proven within the equation under, the robotic’s one-step motion won’t change the situation estimate due to the uniform distribution, the place every area has equal chance to remain and transfer.
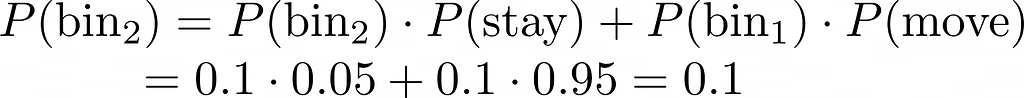
Even when we initially start at a bin with full certainty (100%), the inherent randomness in motion will steadily add noise, main us in the direction of a uniform distribution over time. We have to add info!
3. Sense perform: incorporates measurements that add info utilizing Bayes’ theorem.
After every motion:
For every area:
Area chance at time t+1 given measurement at time t+1 =
Chance of the measurement given the robotic is in that area
x Area chance at time t+1 after motion
x normlization to make sure that all the chances sum to 1.
The sensors reliability is represented with possibilities, since they aren’t 100% correct. The equations under exhibit that when the sensor detects the colour orange, there’s a 90% chance that the robotic is situated in an orange bin, and a ten% chance that the sensor is flawed and the robotic is definitely in a blue bin.

The calculation introduced under illustrates that, in distinction to motion, sensors contribute info and enhance our understanding of the robotic’s location. As an example, as a result of bin 2 just isn’t orange, the chance of the robotic being in it diminishes from 0.1 to 0.02.
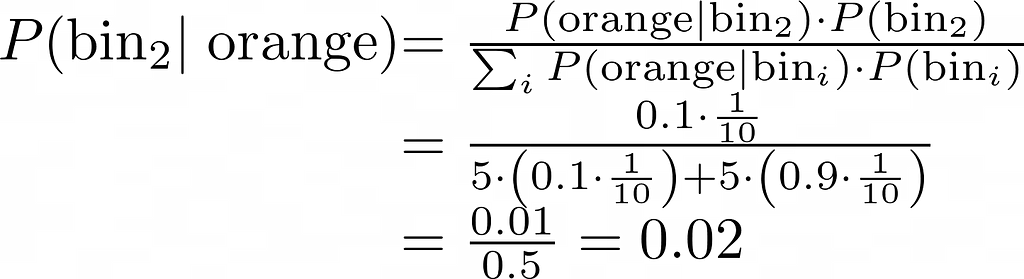
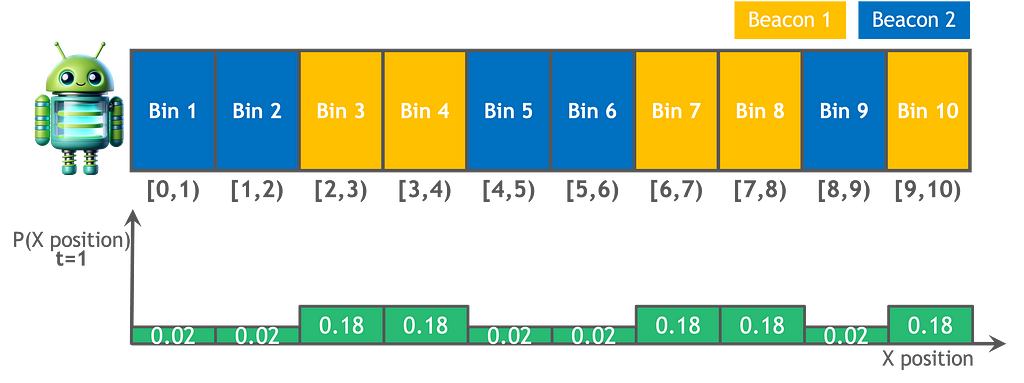
The picture under exhibits the up to date location speculation after incorporating motion and sensors’ information to our preliminary guess.
Ultimate ideas
The place is the robotic? We are able to constantly refine our reply to this query by utilizing recursive bayesian filters, ranging from a uniform distribution that retains all guesses equally possible till selecting the more than likely one.
Bayesian filters assist us measure our confidence within the robotic’s whereabouts, updating this perception by integrating (noisy) sensor information with prior info (the estimated robotic’s place after motion).
Sources:
- These are my abstract notes from the primary lectures of the extremely advocate edX course “Bayesian algorithms for Self-Driving Autos” by Dr.Roi Yozevitch.
- Probabilistic Robotics GitBook: Non parametric filter
- Wikipedia chance, chance idea and bayes theorem
- Daniel Sabinasz’s private weblog on histogram filters
- On-line converter from latex to png.
- Pictures: the robotic avatar was created with Dall-E. All different pictures used on this article have been created by the creator.
How one can end up in a digital world? was initially revealed in In direction of Knowledge Science on Medium, the place persons are persevering with the dialog by highlighting and responding to this story.
[ad_2]